
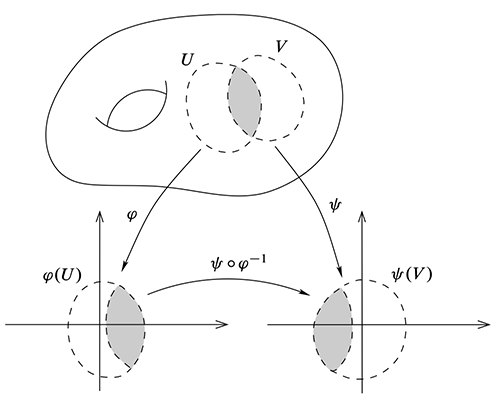
If you walk along a side and get to an edge, things will be too sharp and will no longer look like a plane. Below are the first few that come to mind for me: Note that the manifold is only the surface of these objects and not the interior.Ĭan you think of surfaces that are not manifolds? These surfaces will have problems at some “sharp” points. Here are some common examples of manifolds. Now here’s the rule: From the point of view of the ant, everywhere it walks should look like a flat plane.ĭoes this rule sound familiar? If you’re looking for an application I think this is one that all of us can relate to we live on a manifold! A sphere is one of the simplest examples of a manifold in three dimensions. This manifold could be curvy, twisty, or even have holes in it. Suppose there is a small ant walking along a manifold in three dimensions. Manifolds exist in any dimension, but for the sake of simplicity, let’s think about a three-dimensional space. The best way to understand this property is through example. To be a manifold, there’s one important rule that needs to be satisfied. Manifolds describe a vast number of geometric surfaces. Show how manifolds are used in data science.Visualize examples of manifolds in various contexts.Explain what a manifold is and give a conceptual definition.Manifolds are visual by nature, so everyday examples are abundant. Here’s the good news: It’s very likely you already understand what a manifold is. I claim that a super useful step in answering this question is understanding what a manifold is. How do I spatially represent my data in an accurate and meaningful way?

As more and more data accumulates, it becomes harder to answer the following question: Data science requires an insightful understanding of data.


 0 kommentar(er)
0 kommentar(er)
